Deep Learning Final Project - Conditional Diffusion Model for Brain MR Images
Introduction
In the past few years, generative AI has gained immense public interest, particularly due to the introduction of image generation models as DALL-E, Midjourney, and Stable Diffusion. Known as diffusion models or score-based generative models, these approaches are very powerful because of their ability to conditionally generate new images that fit a given text prompt.
However, many other applications of diffusion models are areas of ongoing research. In medical imaging, diffusion models could be used along with conditional inputs, such as patient data, to generate images with specific desired characteristics. For example, given a dataset of magnetic resonance (MR) images along with class labels for each image, a conditional diffusion model could be used to generate images of a certain class. The goal of this project was to demonstrate this on a small scale, by training a diffusion model to conditionally generate MR images of different contrasts.
Background
A denoising diffusion probabilistic model (DDPM) is a kind of latent variable model trained using variational inference. They can be considered as a method of sampling a probability distribution which is difficult to learn directly, using an approach similar to Langevin dynamics. By introducing conditioning inputs as well as mechanisms such as cross-attention to guide the diffusion process, diffusion models can be used as conditional image generators.
A few works have explored the use of diffusion models in the MR image reconstruction setting. Chung and Ye proposed a score-based diffusion model for image reconstruction [1], and Jalal et al. proposed an annealed Langevin dynamics approach [3]. Jalal et al. required fully-sampled k-space data to learn the score function, while Chung and Ye required only magnitude images. Both approaches attempt to learn a score function and use Langevin dynamics to sample from the posterior distribution of images.
I completed this project for ECE:5995 Applied Machine Learning at UIowa. Originally, I was interested in diffusion models for inverse problems such as MRI reconstruction, but due to time constraints, I focused on image generation. In this project, I developed a diffusion model to generate brain MR images with different contrasts based on a conditioning input vector.
Approach
Diffusion, as defined in [6], is the forward process in which an image \(x_0\) is slowly corrupted over \(T\) timesteps with Gaussian noise of increasing variance, until all structure in the image is destroyed and the image is indistinguishable from a sample of Gaussian noise \(z\) from the distribution \(p(z) = \mathcal{N}(z; \mathbf{0}, \mathbf{I})\). Given a variance schedule \(\beta_1,...,\beta_T\) the transitions between each step in this process can be defined as \(q_t(x_t \ \vert x_{t-1}) = \mathcal{N}(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_t \mathbf{I})\).
 Illustration of forward and reverse diffusion processes
Illustration of forward and reverse diffusion processes
As shown by Ho et al., the forward process posteriors can be defined as
where \(\alpha_t = 1 - \beta_t\) and \(\bar{\alpha}_t = \prod_{s=1}^{t} \alpha_s\).
The denoising diffusion probabilistic model (DDPM) introduced by Ho et al. is a class of latent variable models that learn the reverse transitions \(p_\theta(x_{t-1} \ \vert x_{t}) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \Sigma_\theta(x_t,t)\) by Algorithm 1 shown below.
The intuition behind this algorithm is that a deep neural network is trained as a denoiser. The input to the network is a set of images with Gaussian noise added to them, with the variance of the noise randomly selected from the \(\beta_t\) variance schedule. The network is trained to predict the noise given the noisy image and the timestep \(t\). The loss function is defined as the mean squared error between the predicted noise and the true added noise.
 Training and sampling algorithms for DDPM (Ho et. al)
Training and sampling algorithms for DDPM (Ho et. al)
The trained denoiser can then be used for each transition in the reverse diffusion process, to start from a sample of Gaussian noise and gradually remove noise over many timesteps, until a clean image is produced. This sampling process is described by Algorithm 2. This image can be considered a sample from the original distribution of images.
The U-net implementation was based on Conditional Diffusion MNIST implementation [7]. The embeddings in this network are simple fully connected networks. The network architecture was modified to accept complex-valued input, and the class label context embedding was also disabled.
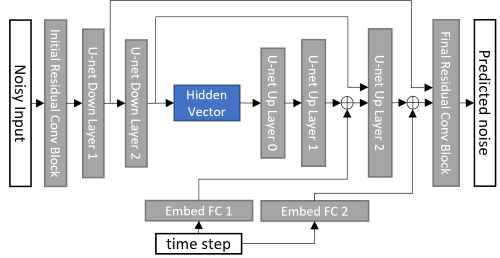 U-net architecture used for unconditional DDPM
U-net architecture used for unconditional DDPM
This approach was first used to train a DDPM for unconditional image generation. Training data was selected from the FastMRI multicoil brain dataset. The training dataset consisted of data with 4 different contrasts. 10 subjects of each contrast were selected, for a total of 40 subjects. After successfully training an unconditional DDPM, the U-net architecture was modified to once again include class label context embeddings. This architecture was then used in a conditional DDPM.
However, there were some limitations in my implementation. Although I added support for complex images, I eventually decided to use magnitude images, and I also downsampled them by a factor of 2, in order to improve the speed of the training and decrease the memory usage of the DDPM.
Results
The conditional DDPM was able to successfully generate reasonable brain MR images of different desired contrasts. An animated example of the sampling process is shown below.

You can read my full write-up of the project here or look at my slides for more details.
References
[1] Chung, H., Ye, J.C., 2022. Score-based diffusion models for accelerated MRI.
[2] Ho, J., Jain, A., Abbeel, P., 2020. Denoising Diffusion Probabilistic Models.
[3] Jalal, A., Arvinte, M., Daras, G., Price, E., Dimakis, A.G., Tamir, J., 2021. Robust compressed sensing MRI with deep generative priors.
[4] Rogge, N., Rasul, K., 2022. The Annotated Diffusion Model, Blog post.
[5] Rombach, R., Blattmann, A., Lorenz, D., Esser, P., Ommer, B., 2022. High-Resolution Image Synthesis with Latent Diffusion Models.
[6] Sohl-Dickstein, J., Weiss, E., Maheswaranathan, N., Ganguli, S., 2015. Deep unsupervised learning using nonequilibrium thermodynamics.
[7] TeaPearce. Conditional Diffusion MNIST GitHub repository.